Hungarian Mathematics Education

The Fasori Gimnazium in Budapest, while it was open between 1864 and 1952, might fairly be claimed to be the best high school in the world. It educated Eugene Wigner, John von Neumann, Edward Teller, Alfred Haar, and John Harsanyi.

So it might be useful to know what they were doing right.

Laszlo Ratz, who designed the curriculum, was the driving force behind the school.  He founded the high school math journal KoMaL, which presented challenging problems so students could write in solutions.  The journal is still in print; you can see sample problems here. Harsanyi and Erdos, along with other prominent mathematicians, were especially good at these competitions.

Ratz also cultivated personal relationships with his most talented students, inviting them to his house and giving them book recommendations.

Here is some biographical information about Ratz, which gives some insight into his ideas on curriculum.  

The basic principle of the Fasori Gimnazium was that students were presented with examples first, and rules for how to solve the problem only after they’d tried to figure it out for themselves.  They also practiced with real statistics, from things like national railway schedules and tables of wheat production. 

Ratz had a particular axe to grind about calculus: he insisted that the concept of derivatives be taught by starting with finite differences.  

Wigner’s recollections about high school noted that they learned Latin, poetry, German, French, botany and zoology, and physics from a history-of-science perspective.  The physics teacher had written his own textbook. He remembered Ratz as exceptionally friendly and encouraging, giving private lessons to von Neumann and lots of books to himself.

It’s hard to determine which, if any, of these things made the Fasori Gimnazium special. But it does point in some useful directions. One-on-one attention from exceptional teachers, a focus on problem-solving and examples, math contests.  It matches my intuition that you only really understand a mathematical concept when you’ve computed it by hand with examples.  

The Calderon-Zygmund Decomposition as Metaphor

The Calderon-Zygmund decomposition is a classic tool in harmonic analysis.

It’s also a part of a reframe of how I think since I started being immersed in this field.

The basic statement of the lemma is that all integrable functions can be decomposed into a “good” part, where the function is bounded by a small number, and a “bad” part, where the function can be large, but locally has average value zero; and we have a guarantee that the “bad” part is supported on a relatively small set.

Explicitly,

Let and let .  Then there exists a countable collection of disjoint cubes such that for each $j$

(that is, the average value of f on the “bad” cubes is not too much bigger than )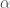

(that is, we have an upper bound on the size of the “bad” cubes)

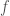and for almost all x not in the union of the . In other words, is small outside the cubes, the total size of the cubes isn’t too big, and it’s not that big even on the cubes.

In particular, if we define

outside the cubes, on each cube, and , then 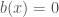outside the cubes, and has average value zero on each cube.  The “good” function 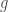is bounded by 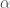; the “bad” function 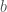is only supported on the cubes, and has average value zero on those cubes.

Why is this true? The basic sketch of the proof  involves taking a big grid of cubes, asking on each one if the average of 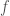is less than 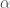or not; if not, the cube is a “bad” cube and we make it one of the , and if not, we keep subdividing, each cube being subdivided into 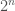daughter cubes.

The intuition here is that functions which are more or less regular (an integrable function has to decay at infinity and not be too singular at zero) can be split into a “good” part that’s either small or locally constant, and a “bad” part that can be wiggly, but only on small regions, and always with average value zero on those regions.

This is the basic principle behind multiscale decompositions.  You take a function on, say, the plane; you decompose it into a “gist” function which is constant on squares of size 1, and a “wiggle” function which is the difference. Then throw away the gist, look at the wiggle, look at squares of side-length 1/2, and again decompose it into a gist which is constant on squares and a wiggle which is everything else.  And keep going.  Your original function is going to be the sum of all the wiggles — or all the gists, depending on how you want to look at it.

But the nice thing about this is that you’re only using local information.  To compute 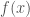, you need to know what size-1 box is in, for the first gist, and then which size-1/2 box, for the first wiggle, and then which size-1/4 box, for the second wiggle, and so on, but you only need to know the wiggles and gists in those boxes.  And if the value of f changed outside the box, the decomposition and approximate value of 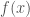wouldn’t change.

So how does this reframe how you see things in the real world?

Well, there are endless debates about whether you “can” capture a complex phenomenon with a simple model.  Can human behavior “really” be reduced to an algorithm? Can you “really” describe economics or biology with equations?  Is this the “right” definition to capture this idea?

To my view, that’s a wrong question. The right question is always “How much information do I lose by making this simplifying approximation?”  A “natural” degree of roughness of your approximation is the turning point where more detail won’t give you much more accuracy.

Multiscale decompositions give you a way of thinking about the coarseness of approximations.

In regions where a function is almost constant, or varying slowly, one layer of approximation is pretty good. In regions where it fluctuates rapidly and at varying scales (think “more like a fractal”), you need more layers of approximation.  A function that has rapid decay in its wavelet coefficients (the “wiggles” shrink quickly) can be approximated more coarsely than a function with slow decay.  These are the functions where the “bad part” of the “bad part” of the “bad part” and so on (in the Calderon-Zygmund sense) remains fairly big rather than rapidly disappearing.  (Of course, since the “bad part” is restricted to cubes, you can compute this separately in each cube, and require a different level of accuracy in different parts of the domain of the function.)

Definitions are approximations. You can define a category by its prototypical, average member, and then define subcategories by how they differ from that average, and sub-sub-categories by how they differ from the average of the sub-categories.

The hierarchical structure allows you to be much more efficient; you can skip the extra detail when it’s not warranted.  In fact, there’s a fair amount of evidence that this is how the human brain structures information.

The language of harmonic analysis deals a lot with how to relate measures of regularity (basically, bounds on integrals, or measures of smoothness) with measures of coefficient decay (basically, how deep down the tree of successive approximations do you need to go to get a good estimate). Calderon-Zygmund decomposition is just one of the simpler cases.  But the basic principle of “nicer functions permit rougher approximations” is a really good framing device to dissolve questions about choosing definitions and models. Debates about “this model can never capture all the complexity of the real thing” vs. “this model is a useful simplification” should be replaced by debates about how amenable the phenomenon is to approximation, and which model gives you the most accurate picture relative to its simplicity.

How I Read: the Jointed Robot Metaphor

“All living beings, whether born from eggs, from the womb, from moisture, or spontaneously; whether they have form or do not have form; whether they are aware or unaware, whether they are not aware or not unaware, all living beings will eventually be led by me to the final Nirvana, the final ending of the cycle of birth and death. And when this unfathomable, infinite number of living beings have all been liberated, in truth not even a single being has actually been liberated.” The Diamond Sutra

What do you do when you read a passage like this?

If you’re not a Buddhist, does it read like nonsense?

Does it seem intuitively true or deep right away?

What I see when I read this is a lot of uncertainty.  What is a living being that does not have form?  What is Nirvana anyway, and could there be a meaning of it that’s not obviously incompatible with the laws of physics?  And what’s up with saying that everyone has been liberated and nobody has been liberated?

Highly metaphorical, associative ideas, the kind you see in poetry or religious texts or Continental philosophy, require a different kind of perception than you use for logical arguments or proofs.

The concept of steelmanning is relevant here. When you strawman an argument, you refute the weakest possible version; when you steelman an argument, you engage with the strongest possible version.   Strawmanning impoverishes your intellectual life. It does you no favors to spend your time making fun of idiots.  Steelmanning gives you a way to test your opinions against the best possible counterarguments, and a real possibility of changing your mind; all learning happens at the boundaries, and steelmanning puts you in contact with a boundary.

A piece of poetic language isn’t an argument, exactly, but you can do something like steelmanning here as well.

When I read something like the Diamond Sutra, my mental model is something like a robot or machine with a bunch of joints.

Each sentence or idea could mean a lot of different things. It’s like a segment with a ball-and-socket joint and some degrees of freedom.  Put in another idea from the text and you add another piece of the robot, with its own degrees of freedom, but there’s a constraint now, based on the relationship of those ideas to each other.  (For example: I don’t know what the authors mean by the word “form”, but I can assume they’re using it consistently from one chapter to another.)  And my own prior knowledge and past experiences also constrain things: if I want the Diamond Sutra to click into the machine called “Sarah’s beliefs,” it has to be compatible with materialism (or at least represent some kind of subjective mental phenomenon encoded in our brains, which are made of cells and atoms.)

If I read the whole thing and wiggle the joints around, sooner or later I’ll either get a sense of “yep, that works, I found an interpretation I can use” when things click into place, or “nope, that’s not actually consistent/meaningful” when I get some kind of contradiction.

I picture each segment of the machine as having a continuous range of motion. But the set of globally stable configurations of the whole machine is discrete. They click into place, or jam.

You can think of this with energy landscape or simulated-annealing metaphors. Or you can think of it with moduli space metaphors.

This gives me a way to think about mystical or hand-wavy notions that’s not just free-association or “it could mean anything”, which don’t give me enough structure.  There is structure, even when we’re talking about mysticism; concepts have relationships to other concepts, and some ways of fitting them together are kludgey while others are harmonious.

It can be useful to entertain ideas, to work out their consequences, before you accept or reject them.

And not just ideas. When I go to engage in a group activity like CFAR, the cognitive-science-based self-improvement workshop where I spent this weekend, I naturally fall into the state of provisionally accepting the frame of that group.  For the moment, I assumed that their techniques would work, engaged energetically with the exercises, and I’m waiting to evaluate the results objectively until after I’ve tried them.  My “machine” hasn’t clicked completely yet — there are still some parts of the curriculum I haven’t grokked or fit into place, and I obviously don’t know about the long-term effects on my life.  But I’m going to be wiggling the joints in the back of my mind until it does click or jam.  People who went into the workshop with a conventionally “skeptical” attitude, or who went in with something like an assumption that it could only mean one thing, tended to think they’d already seen the curriculum and it was mundane.

I’m not trying to argue for credulousness.  It’s more like a kind of radical doubt: being aware there are many possible meanings or models and that you may not have pinned down “the” single correct one yet.

Why Otium?

One of my more controversial beliefs is that speculative thinking is valuable.

This goes against the grain of the ideal that scientists and other professionals should be specialists.  As a mathematician, so says the “specialist ethos”, I should make careful and precise statements about my field of mathematics, and remain deliberately agnostic about everything else.  Over time, I can become an authority in my field, and my statements will be an expert’s judgments; until then, what I think is just “opinion”, and opinions are basically worthless.  Every newspaper reader has an opinion; the Internet is full of idiots with opinions; if you want a real answer, ask an expert.

The “specialist ethos” is, I believe, overly authoritarian and harmful to free inquiry.  Sure, uninformed opinions are less reliable, and it’s valuable to be aware when you don’t know what you’re talking about.  But intellectuals often can make valid contributions to fields outside their own.  And discussion about speculative, early-stage ideas is critical to the development of new paradigms, scientific fields, and technologies.  Speculation is looser and more uncertain than proof or experiment, but if we don’t do it, we calcify.

The alternative to a specialist ethos is a philosophical ethos.  The classical world valued otium, literally meaning leisure, but with a connotation of intellectual contemplation outside of the constraints of public life.  Seneca writes of curiosity for its own sake, and the virtue of the contemplative life as an occasion for exploration and leaving knowledge for posterity.

For most of Western history, the intellectual was not a specialist but a philosopher.  Speculative inquiry was considered a virtue.  And the practice of philosophy was considered incompatible with participation in public life; the Stoics believed that one should balance the active with the contemplative, but believed that a “commonwealth” would inevitably persecute a genuine philosopher as Athens persecuted Socrates. To do philosophy, you would have to retire, for some time, to a private estate, away from the pressures of politics and business.

And so, to blogging. A WordPress site isn’t a villa (unfortunately), and I’m not a Roman philosopher.  But a place for speculative thinking and discussion, apart from professional competition, remains valuable.

When I write here, I’ll write as a human being thinking about things, not as a professional.  It’ll be filtered through the lens of my education, which means there will be some math, at varying levels of technicality, but there’ll also be a lot of hand-waving, rough ideas, metaphors, and wild guesses.  I’ll be wrong sometimes.  I’ll facepalm at my own mistakes.  I’ll talk about things like biology and business, where I’m a novice, and about things like how thinking works, where in some sense everyone’s an amateur.  And maybe this is an unusual practice, but I think of it as the basic way that a free, complete, thinking human being goes through life.

Happy reading!